Трехмерный Анализ Сложных Акустических Оформлений

Взял на сайте Александра Соколова(Ясного Сокола) и Сергея Каноненко.

1. Введение

Использование современных методов численного моделирования физических процессов позволяет достичь новых результатов, недоступных ранее из-за сложности их моделирования . 3D Acoustic Research поставила своей задачей разработку и внедрение математических численных методов для анализа акустических систем. В результате трехмерного расчета мы моделируем звуковое поле, создаваемое динамиком, что позволяет оценить поведение акустической системы до процесса ее реального воплощения.

Существует множество моделей акустического оформления, которые в своем большинстве имеют нулевую размерность (например. расчет простых акустических оформлений типа «закрытый ящик», или «фазоинвертор»), или первого порядка, в которой учитываются изменения физических величин только вдоль одного направления (пример - одномерное уравнение рупора). Тем не менее, множество акустических систем (например, рупорные системы, трансмиссионные линии, экраны сложной формы), имеют сложную трехмерную форму, и указанные выше модели для них имеют ограничения. Для подобных систем только трехмерный анализ способен дать полноценный результат. Рассматриваемый метод также имеет значение для анализа максимальных интенсивностей звукового поля не только снаружи, но и внутри АС.

2. Как это работает

d^2(φ)/dt^2+ c^2* Δ (φ) =0

где φ – потенциал волны. Уравнение в частных производных для решения на компьютере переписывается в виде уравнения в конечных разностях. Для продвижения решения во времени в памяти хранятся значения во времени на текущем шаге t и на предыдущем шаге t-1.

Оформление АС задается в виде жестких элементов (стенок) в узлах сетки, отражающих волну. Условием отражения является нулевое значение градиента вдоль нормали, направленной к поверхности стенки.

Граничными условиями вблизи поверхности диффузора является условие равенства нормальной компоненты скорости частиц в волне и скорости движение диффузора. При этом само движение диффузора описывается уравнением движения Ньютона под действием электромагнитной силы со стороны магнита, упругости, трения в подвесе и силы инерции. Учитывается, что поле давления, создаваемой вокруг диффузора, может быть неоднородным.

3. Как это отображается

Нами разработан графический интерфейс с использованием трехмерного представления, позволяющий визуализировать полученные результаты. Для расчета можно задать практически произвольное оформление АС в виде набора последовательных сечений произвольной формы, которые импортируются в трехмерную расчетную сетку. Параметры динамика задаются через физические параметры (такие как масса, упругость подвеса, сила магнита), либо через общепринятые параметры Тилля-Смола. Представление результатов является трехмерным. После окончания расчета можно визуализировать поле волны, значение акустического давления, фазы по всей области расчета в зависимости от заданной частоты. Перемещение виртуального микрофона позволяет определить АЧХ, создаваемого АС, в заданной точке пространства.

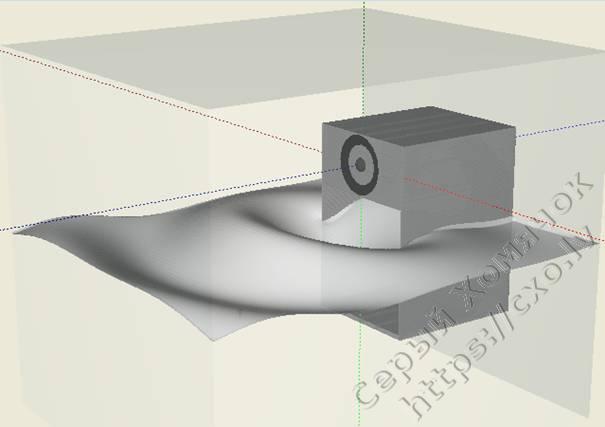
На Рис. 1 показано сложное акустическое оформление в виде «обратный рупор», импортированного в трехмерную сетку для расчета.

Рис1. Обратный рупор

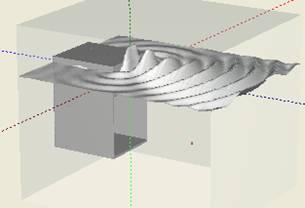
После выполнения расчета по заданному интервалу частот визуализируется поле звуковой волны (см Рис 2) , среднеквадратичное давление, создаваемое АС, фаза волны (Рис.5). Для заданного на рис.1 рупора расчет выполнялся на сетке 180 х 150 х 150, имеющей размер одного элемента 1 см.

Графическое представление результатов создается в некоторой плоскости, которая делит область расчета. Плоскость сечения задается произвольно, с помощью мыши может перемещается по области численной сетки, при этом изменяются отображаемые результаты.

Визуализатор позволяет рассматривать изображение под разными углами и с изменением масштаба увеличения.

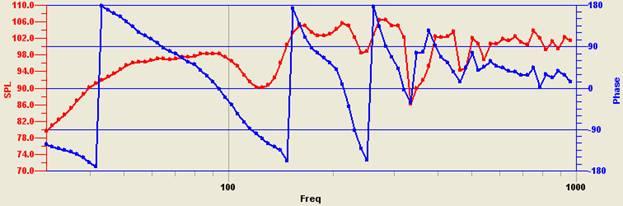
Перемещение виртуального микрофона в произвольную точку пространства рядом с АС позволяет построить график АЧХ и ФЧХ в точке положения микрофона.

500 Гц

200 Гц

Рис.2. Поле звуковой волны, создаваемой рупором.

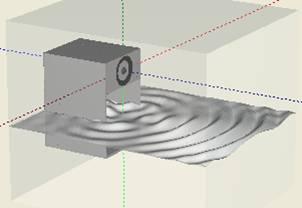Рис. 3 . Поле волны (2 кГц) в разных сечениях по высоте рупора

Рис. 3. Среднее звуковое давление (SPL) по области расчета, дБ. Плоскость сечения показана сеткой, а величина давления пропорциональна расстоянию между сеткой и верхней поверхностью

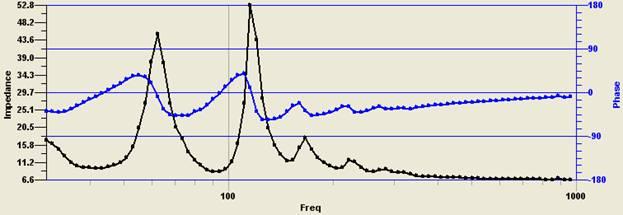
Рис. 4. АЧХ и импеданс в точке положения микрофона

4. Вычисления на CUDA

Появление параллельной вычислительной платформы CUDA существенно расширяет возможности метода численного трехмерного моделирования для проектирования акустических систем.

Для пользователя, установившего видео карту с поддержкой CUDA, появится возможность ускорить расчет в десятки раз (в первоначальном релизе программы опция СUDA отсутствует).

Для видеокарт с поддержкой CUDA средней ценовой категории (например NVIDIA GTX 260) нам удалось получить приемлемые результаты с общим временем расчета порядка 10-30 мин. Используемая платформа позволяет также получить результаты, которые ранее можно было рассматривать как практически недоступные (при дальнейшем увеличении размера сетки и уменьшении ее элемента).

Использование платформы CUDA, по нашим проведенным оценкам, на данном уровне технологии позволяет использовать численную сетку порядка 1 см. Такая точность уже является во многих случаях достаточной для моделирования акустических систем в области низких и средних частот (до 1 кгц), если сечение между каналами акустической системы больше 1 см.

Приведенные выше примеры были рассчитаны на CUDA на численной сетке 180 х 150 х 150 элементов по трем координатам, с шагом сетки 1 см. На графической карте средней ценовой категории (NVIDIA GTX260 – порядка 200 дол) расчет в диапазоне частот 20 -1000 Гц с шагом в 1/6 октавы и временем интегрирования 60 миллисекунд для каждого значения частоты занял 10 мин 38 сек. Данный результат нам представляется достаточным для практического использования разработанного инструмента в исследовательских целях при проектировании акустической системы.

Для анализа эффективности платформы CUDA мы создали два вычислительных ядра –построенного на платформе CUDA и без. Второе ядро написано на С++ с компиляцией под Visual Studio 2008, и выполняется на одном процессорном ядре без распараллеливания по ядрам центрального процессора персонального компьютера. Также во втором случае не использовалась оптимизация SSE.

Сравнение двух вычислительных модулей представлено в табл.1. Как следует из таблицы, достигаемое ускорение на платформе CUDA составляет порядка 27 раз на сетках большого размера.

Табл.1 Ускорение, NVIDIA GTX260 по отношению к Pentium 2.4 ГГц (одно ядро)

Скачать у меня, не факт что свежее.

Скачать с сайта разработчиков.